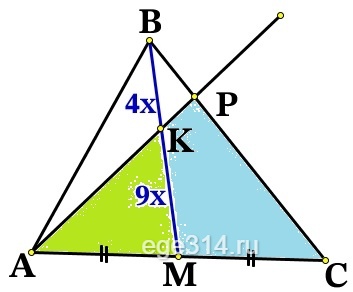
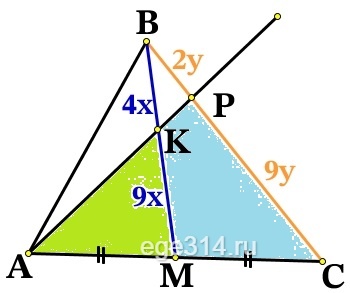
Решение №2190 В треугольнике АВС на его медиане ВМ отмечена точка К так, что ВК : КМ = 4 : 9.

В треугольнике АВС на его медиане ВМ отмечена точка К так, что ВК : КМ = 4 : 9. Прямая АК пересекает сторону ВС в точке Р. Найдите отношение площади треугольника AKM к площади четырёхугольника KPCM.

Источник: ОГЭ Ященко 2022 (36 вар)

Решение:

Обозначим S_ΔABC, как S.
Треугольники ABM и MBC равновеликие, т.к. образованы медианой BM, значит имеют равную площадь:

$S_{\Delta ABM}=S_{\Delta MBC}=\frac{S}{2}$

Основание MK треугольника АКM, составляет $\frac{9}{13}$ основания ВМ треугольника ΔАВМ (9 частей из 13 (9 + 4) частей), тогда S_ΔАКM равна (высота треугольников к этим основаниям общая):

$S_{\Delta AKM}=\frac{9}{13}\cdot S_{\Delta ABM}=\frac{9}{13}\cdot\frac{S}{2}=\frac{9S}{26}$

По теореме Менелая в треугольнике ΔМВС:

$\frac{MK}{KB}\cdot \frac{BP}{PC}\cdot \frac{CA}{AM}=1$

$\frac{9}{4}\cdot \frac{BP}{PC}\cdot \frac{2AM}{AM}=1$

$\frac{9}{4}\cdot \frac{BP}{PC}\cdot \frac{2}{1}=1$

$\frac{9}{2}\cdot \frac{BP}{PC}=1$

$\frac{BP}{PC}=\frac{1}{\frac{9}{2}}$

$\frac{BP}{PC}=\frac{2}{9}$

Из отношения площадей треугольников ΔВРК и ΔВМС выразим S_ΔBPK. Если угол одного треугольника равен углу другого треугольника (общий ∠В), то площади этих треугольников относятся как произведения сторон, заключающих равные углы (из площади треугольников через синус угла и две стороны):

$\frac{S_{\Delta BPK}}{S_{\Delta BMC}}=\frac{\frac{1}{2}\cdot sin\angle B\cdot BK\cdot BP }{\frac{1}{2}\cdot sin\angle B\cdot BM\cdot BC}=\frac{ BK\cdot BP}{BM\cdot BC}$