Решение №3156 В параллелограмме ABCD диагонали являются биссектрисами его углов, AB = 45, AC = 72.

В параллелограмме ABCD диагонали являются биссектрисами его углов, AB = 45, AC = 72. Найдите BD.

Источник: Ященко ЕГЭбаза 2023 (30 вар).

Решение:

Если диагонали параллелограмма являются биссектрисами его углов, то такой параллелограмм является ромбом, а диагонали пересекаются под прямым углом:

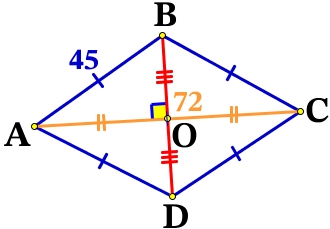
Рассмотрим прямоугольный ΔABO, в котором известна гипотенуза AB = 45 и катет AO = AC/2 = 72/2 = 36 (диагонали в точке пересечения делятся пополам). Найдем BO по теореме Пифагора:

AB² = BO² + AO²
45² = BO² + 36²
2025 = BO² + 1296
2025 – 1296 = BO²
729 = BO²
BO = √729 = 27

Найдём диагональ BD:

BD = 2∙27 = 54

Ответ: 54.