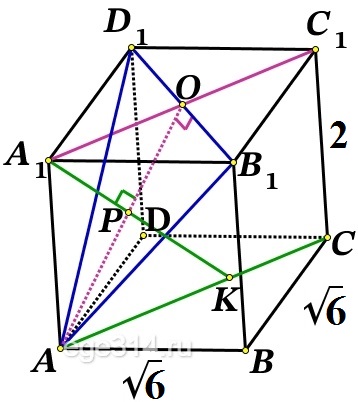
Решение №2584 В правильной призме ABCDA1B1C1D1 с основанием ABCD боковое ребро равно 2, а сторона основания равна √6.

Решение:

а) Доказать: АК:КС = 2:1. Прямая l это прямая А₁К. Построим рисунок по условию задачи:

    А₁К⊥D₁B₁, A₁K⊥AO, AO⊥D₁B₁ (по теореме о 3-х перпендикулярах).
    Призма правильная четырёхугольная, значит в основании лежит квадрат со сторонами √6.
    Найдём по теореме Пифагора в ΔАВС диагональ основания АС:

AC=\sqrt{AB^{2}+BC^{2}}=\sqrt{(\sqrt{6})^{2}+(\sqrt{6})^{2}}=\sqrt{12}=\sqrt{3\cdot 4}=2\sqrt{3}
AC = A₁С₁ = 2\sqrt{3}

    Точка пересечения диагоналей квадрата О делит их пополам:

А₁О = ОС₁ = А₁С₁/2 = \frac{2\sqrt{3}}{2}=\sqrt{3}

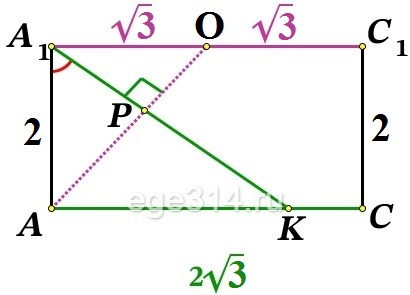
    Построим прямоугольное сечение АСС₁А₁:

    В прямоугольном ΔА₁АО по теореме Пифагора:

AO=\sqrt{A_{1}O^{2}+A_{1}A^{2}}=\sqrt{\sqrt{3}^{2}+2^{2}}=\sqrt{7}

    В прямоугольном ΔА₁АО из двух формул для нахождения площади треугольника найдём высоту А₁Р:

S_ΔА1АО = S_ΔА1АО 
\frac{1}{2}\cdot A_{1}A\cdot A_{1}O=\frac{1}{2}\cdot AO\cdot A_{1}P
\frac{1}{2}\cdot 2\cdot \sqrt{3}=\frac{1}{2}\cdot \sqrt{7}\cdot A_{1}P
2\cdot \sqrt{3}= \sqrt{7}\cdot A_{1}P
A_{1}P=\frac{2\cdot \sqrt{3}}{ \sqrt{7}}=2\sqrt{\frac{3}{7}}

    В прямоугольном ΔА₁АP по теореме Пифагора:

AP=\sqrt{A_{1}A^{2}-A_{1}P^{2}}=\sqrt{2^{2}-(2\sqrt{\frac{3}{7}})^{2}}=\sqrt{4-\frac{12}{7}}=\sqrt{\frac{16}{7}}=\frac{4}{\sqrt{7}}

    В прямоугольном ΔА₁АP найдём тангенс ∠А₁:

tg\: \angle A_{1}=\frac{AP}{A_{1}P}=\frac{\frac{4}{\sqrt{7}}}{2\sqrt{\frac{3}{7}}}=\frac{2}{\sqrt{3}}

    В прямоугольном ΔА₁АK через тангенс ∠А₁ найдём АК:

tg\: \angle A_{1}=\frac{AK}{A_{1}A}
\frac{2}{\sqrt{3}}=\frac{AK}{2}
AK=\frac{4}{\sqrt{3}}

    Найдём КС:

КС = АС – АК = 2\sqrt{3}-\frac{4}{\sqrt{3}}=\frac{2}{\sqrt{3}}

    Найдём искомое отношение АК:КС:

\frac{AK}{KC}=\frac{\frac{4}{\sqrt{3}}}{\frac{2}{\sqrt{3}}}=\frac{4}{2}=\frac{2}{1}
АК:КС = 2:1

    Что и требовалось доказать.

Ответ: б) arccos\, \frac{2\sqrt{210}}{35}.