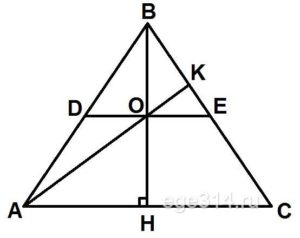
В правильном треугольнике АВС проведена средняя линия DE параллельно АС. Прямая, проходящая через точку А и середину F отрезка DE, пересекает ВС в точке К. Найдите длину отрезка АК, если АС = 9√7.
Источник задания: alexlarin.net
Решение:
Построим треугольник по условию задачи и высоту BH:
Рассмотрим ΔОКЕ и ΔАКС, они подобны по двум равным углам ∠КОЕ = ∠КАС, ∠КЕО = ∠КСА (как соответствующие при двух параллельных сторонах и секущей). Составим соотношение сторон:
Найдём ОЕ, это половина средней линии, которая в свою очередь равна половине основания АС:
Подставим в соотношение сторон:
Значит ОК составляет 1 часть из 4-х частей, обозначим её за х, тогда АО оставшиеся 3 части, т.е. 3х.
Из прямоугольного треугольника АОН найдём значение х. Сторона АО = 3х, АН это половина АС:
ОН составляет половину от ВН, а ВН найдём из прямоугольного ΔABH по теореме Пифагора:
Найдём ОН:
Подставляем и по теореме Пифагора находим из прямоугольного ΔАОН х:
AO2 = AH2 + OH2
Найдём АК:
АК = 4х = 4·5,25 = 21
Ответ: 21.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 2
Оценок пока нет. Поставь оценку первым.
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, чтобы я тебе ответил.