Объём конуса равен 32. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объём меньшего конуса.
Источник: mathege
Решение:
Объём конуса находится по формуле:
V_{конуса}=\frac{1}{3}\pi R^{2}h
Тогда для большего конуса:
V_{б.конус}=\frac{1}{3}\pi R^{2}h=32
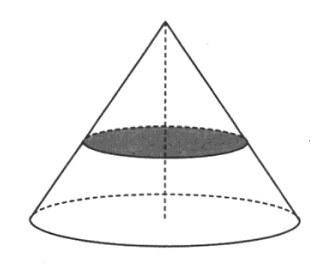
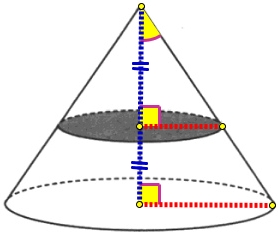
Основание меньшего конуса проведено через середину высоты большего конуса, тогда высота меньшего конуса:
h_{м.конус}=\frac{1}{2}h
Треугольники большего и меньшего конуса подобны по 2-м углам (по 1-му прямому и 1-н общий острый угол при вершине), тогда соответствующие стороны этих треугольников пропорциональны.
Радиусы и высоты конусов, являются сторонами данных треугольников, значит они относятся друг другу одинаково:
h_{м.конус}=\frac{1}{2}h\\R_{м.конус}=\frac{1}{2}R
Найдём объём меньшего конуса:
V_{м.конус}=\frac{1}{3}\pi \cdot (\frac{1}{2}R)^{2}\cdot \frac{1}{2}h=\frac{1}{3}\pi \cdot \frac{1}{4}R^{2}\cdot \frac{1}{2}h=\frac{1}{4}\cdot \frac{1}{2}\cdot \frac{1}{3}\pi R^{2}h=\frac{1}{8}\cdot V_{б.конус}=\frac{1}{8}\cdot 32=4
Ответ: 4.