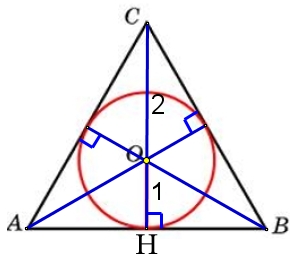
Радиус окружности, вписанной в равносторонний треугольник, равен 15. Найдите высоту этого треугольника.
Источник: ОГЭ Ященко 2023 (36 вар)
Решение:
Центр вписанной окружности в равносторонний треугольник, является точкой пересечения высот. Высоты делятся точкой пересечения О в отношении 2:1, считая от вершины.
Вся высота СН состоит из 3-х частей (2:1; 2 + 1 = 3), а радиус ОН = 15 это 1 часть. Найдём высоту СН:
СН = 3·r = 3·OH = 3·15 = 45
Ответ: 45.