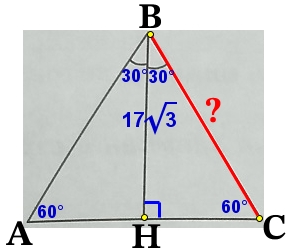
Биссектриса равностороннего треугольника равна 17√3. Найдите сторону этого треугольника.
Источник: ОГЭ Ященко 2022 (50 вариантов)
Решение:
В равностороннем треугольнике все углы равны 60°, а биссектриса является так же высотой.
Тогда:
∠АВН = ∠СВН = 60°/2 = 30°
∠ВНС = 90°
В прямоугольном треугольнике ΔНВС, через косинус угла ∠СВН найдём искомую сторону ВС.
Косинус острого угла прямоугольного треугольника – это отношение прилежащего катета к гипотенузе.
cos\angle CHB=\frac{BH}{BC}\\cos\:30°=\frac{17\sqrt{3}}{BC}\\\frac{\sqrt{3}}{2}=\frac{17\sqrt{3}}{BC}{\color{Blue} |:\sqrt{3}}\\\frac{1}{2}=\frac{17}{BC}
ВС = 2·17 = 34
Ответ: 34.