Решение №1869 Игральную кость бросили один или несколько раз. Оказалось, что сумма всех выпавших очков равна 4.

Решение:

Р_{4 очка 1 бросок} = Р_{4 очка}·Р_{1 бросок} (1)

    Вероятность того, что 4 очка выпало при 1 броске (Р_{4 очка 1 бросок}):

\frac{1}{6} 

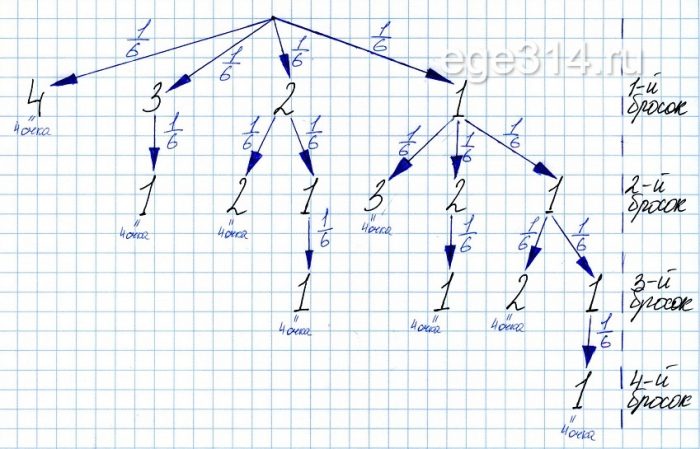
    Изобразим все случаи деревом вариантов при которых выпало 4 очка (Р_{4 очка}):

    Посчитаем чему равна эта вероятность:

\frac{1}{6}+\frac{1}{6^{2}}+\frac{1}{6^{2}}+\frac{1}{6^{3}}+\frac{1}{6^{2}}+\frac{1}{6^{3}}+\frac{1}{6^{3}}+\frac{1}{6^{4}}=\frac{1}{6}+\frac{3}{6^{2}}+\frac{3}{6^{3}}+\frac{1}{6^{4}}=\frac{1\cdot 6^{3}+3\cdot 6^{2}+3\cdot 6+1}{6^{4}}=\frac{343}{6^{4}} 

    Подставим найденные значения в формулу (1) и найдём вероятность того, что был сделан 1 бросок:

Р_{4 очка 1 бросок} = Р_{4 очка}·Р_{1 бросок}

\frac{1}{6}=\frac{343}{6^{4}}\cdot P_{1 \: бросок}
P_{1 \: бросок}=\frac{1}{6}:\frac{343}{6^{4}}=\frac{1}{6}\cdot \frac{6^{4}}{343}=\frac{6^{3}}{343}=\frac{216}{343}\approx 0,629..\approx 0,63

Ответ: 0,63.