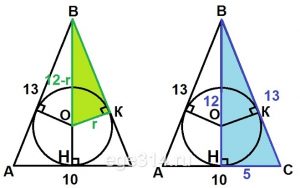
В равнобедренном треугольнике основание равно 10 см, а боковая сторона равна 13 см. найдите радиус окружности, вписанной в этот треугольник.
Решение:
Проведём радиусы окружности к сторонам ΔАВС, стороны являются касательными и перпендикулярны с радиусами.
ВН является высотой, медианой и биссектрисой равнобедренного ΔАВС и проходит, через центр окружности О.
Т.к. ВН медиана найдём НС:
Из прямоугольного ΔВНС, по теореме Пифагора, найдём ВН:
ВС2 = ВН2 + НС2
132 = ВН2 + 52
ВН2 = 169 – 25 = 144
ВН = √144 = 12
Треугольники ΔВКО и ΔВНС подобны по двум равным углам: ∠В – общий, ∠ОКВ = СНВ = 90°, прямые.
Составим пропорцию, для соответствующих сторон треугольников и найдём радиус r:
13r = 5·(12 – r)
13r = 60 – 5r
13r + 5r = 60
18r = 60
Ответ: .