Решение №500 В правильной треугольной пирамиде SABC сторона основания AB=8√3, а боковое ребро SA=√73.

Решение:

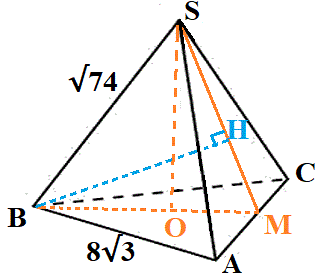
     Расстояние от точки В до плоскости SAC – это перпендикуляр BH, его нам и надо найти.

AM=\frac{AC}{2}=\frac{8\sqrt{3}}{2}=4\sqrt{3}

     Треугольник АВМ прямоугольный, т.к. ВМ перпендикуляр, по теореме Пифагора найдём ВМ:

АМ² + ВМ² = ВА²
(4√3)² + ВМ² = (8√3)²
ВМ = 12

     В правильной треугольной пирамиде высота SO падает на медиану BM  и делит её в отношении 2 к 1, тогда ВО = 2х, ОМ = х:

2х + х = 12
х = 4 = ОМ
2х = 8 = ВО

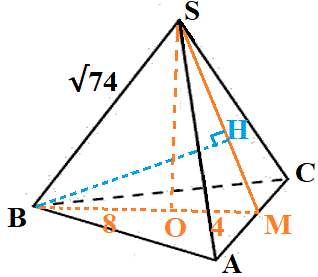
     По теореме Пифагора найдём SO:

SO² + BO² = BS²
SO² + 8² = √74²
SO = 3

     По теореме Пифагора и зная египетский треугольник SM = 5.
     Используя то, что площадь треугольника BSM, можно находить несколькими способами найдём ВН:

S_{BSM}=\frac{1}{2}\cdot SO\cdot BM=\frac{1}{2}\cdot 3\cdot 12=18\\S_{BSM}=\frac{1}{2}\cdot BH\cdot SM\\18=\frac{1}{2}\cdot BH\cdot 5\\18=\frac{5}{2}\cdot BH \\BH=7,2

Ответ: 7,2.