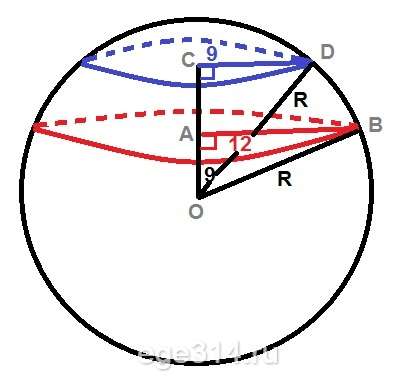
Шар пересечён двумя параллельными плоскостями, расположенными по одну сторону от его центра. Радиус первого сечения равен 12, радиус второго сечения равен 9. Расстояние от центра шара до плоскости первого сечения равно 9. Найдите расстояние между плоскостями сечений.
Решение:
Найдём радиус R шара из прямоугольного ΔAOB по теореме Пифагора:
R2 = OA2 + AB2
R2 = 92 + 122
R2 = 81 + 144 = 255
R = √255 = 15
Прямоугольный ΔCDO состоит из сторон равных 9 и 15 (R), а значит третья сторона как и в прошлом треугольнике равна 12. СО = 12.
Найдём расстояние между сечениями СА:
СА = СО – АО = 12 – 9 = 3
Ответ: 3.