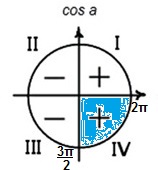
Найдите значение выражения соs α, если tg\alpha=-\frac{\sqrt{21}}{2} и α ∈ (\frac{3\pi}{2};2\pi).
Решение:
tg\alpha=\frac{sin\alpha}{cos\alpha}=-\frac{\sqrt{21}}{2}\\sin\alpha=-\frac{\sqrt{21}}{2}\cdot cos\alpha
По основному тригонометрическому тождеству:
sin^{2}\alpha+cos^{2}\alpha=1\\(-\frac{\sqrt{21}}{2}\cdot cos\alpha)^{2}+cos^{2}\alpha=1\\\frac{21}{4}\cdot cos^{2}\alpha+cos^{2}\alpha=1\\\frac{21}{4}cos^{2}\alpha+1\cdot cos^{2}=1\\cos^{2}\alpha(\frac{21}{4}+1)=1\\cos^{2}\alpha(\frac{21}{4}+\frac{4}{4})=1\\\frac{25}{4}\cdot cos^{2}\alpha=1\\cos^{2}\alpha=1:\frac{25}{4}\\cos^{2}\alpha=\frac{4}{25}\\cos\alpha=±\sqrt{\frac{4}{25}}=±\frac{2}{5}=±0,4
По условию α ∈ (\frac{3\pi}{2};2\pi), там cos α > 0.
Значит cos α = +0,4
Ответ: 0,4.