На рисунке изображены части графиков функций f(x)=\frac{k}{x} и g(x)=\frac{c}{x}+d. Найдите ординату точки пересечения графиков этих функций.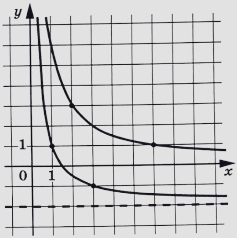
Источник: Ященко ЕГЭ 2023 (36 вар)
Решение:
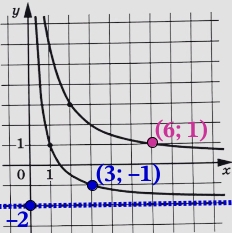
Коэффициент d прибавленный к функции g(x) влияет на сдвиг гиперболы по оси у, гипербола сдвинута на 2 вниз:
d = –2
Подставим координаты точки (3; –1) принадлежащей гиперболе g(x) и найдём c:
g(x)=\frac{c}{x}+d\\-1=\frac{c}{3}-2\\-1+2=\frac{c}{3}\\1=\frac{c}{3}\\c=3
Функция g(x) имеет вид:
g(x)=\frac{3}{x}-2
Подставим координаты точки (6; 1) принадлежащей гиперболе f(x) и найдём k:
1=\frac{k}{6}\\k=6
Функция f(x) имеет вид:
f(x)=\frac{6}{x}
Приравняем функции и найдём их общую точку:
f(x)=g(x)\\\frac{6}{x}=\frac{3}{x}-2\\\frac{6}{x}-\frac{3}{x}=-2\\\frac{3}{x}=-2\\x=\frac{3}{–2}=-1,5
Подставим в любую функцию значение х и найдём ординату (у) точки пересечения графиков:
f(x)=\frac{6}{x}\\f(-1,5)=\frac{6}{–1,5}=-4
Ответ: –4.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.7 / 5. Количество оценок: 114
Оценок пока нет. Поставь оценку первым.
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, чтобы я тебе ответил.
