Решение №168 В правильной четырёхугольной пирамиде боковое ребро равно 7,5, а сторона основания равна 10. Найдите высоту пирамиды.

Решение:

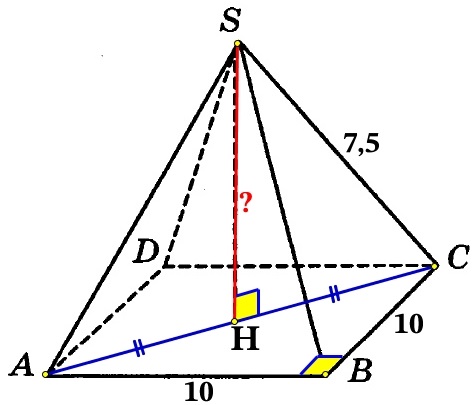
    У правильной четырёхугольной пирамиды в основании лежит квадрат, все его стороны равны и углы прямые. По теореме Пифагора, найдём диагональ АС:

АС² = АВ² + ВС²
АС² = 10² + 10²
АС² = 200
АС² = 4·50
АС = 2√50

    HC является половиной диагонали АС, т.к. точка Н середина диагоналей квадрата, в которой они делятся пополам. Найдём НС:

HC=\frac{AC}{2}=\frac{2\sqrt{50}}{2}=\sqrt{50}

    SH высота пирамиды, тогда ΔSHC прямоугольный, найдём по теореме Пифагора SH:

SC² = HC² + SH²
7,5² = (√50)² + SH²
56,25 = 50 + SH²
56,25 – 50 = SH²
6,25 = SH²
SH = √6,25 = 2,5

Ответ: 2,5.