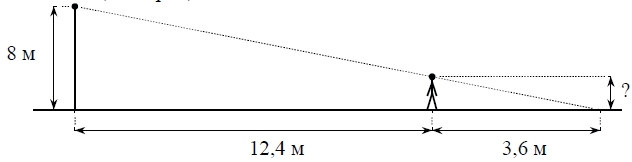
Человек стоит на расстоянии 12,4 м от столба, на котором висит фонарь, расположенный на высоте 8 м. Длина тени человека равна 3,6 м. Какого роста человек (в метрах)?
Источник: statgrad
Решение:
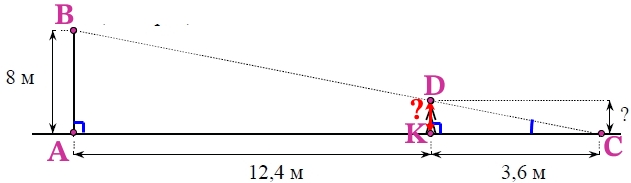
Необходимо найти рост человека DK.
Треугольники ΔАВС и ΔDKC подобны по двум равным углам (∠С –общий, ∠ВАС = DKC, как прямые). В подобных треугольниках, соответствующие стороны пропорциональны:
\frac{AB}{DK}=\frac{AC}{KC}\\\frac{AB}{DK}=\frac{AK+KC}{KC}\\\frac{8}{DK}=\frac{12,4+3,6}{3,6}\\\frac{8}{DK}=\frac{16}{3,6}\:{\color{Blue} |: 8}\\\frac{1}{DK}=\frac{2}{3,6}\\DK\cdot 2=1\cdot 3,6\\DK=\frac{3,6}{2}=1,8\:м
Ответ: 1,8.