Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 10 и 1, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
Источник: Пробный ЕГЭ 2017
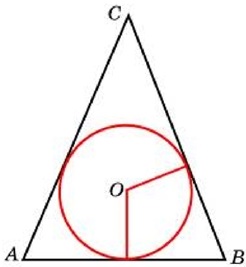
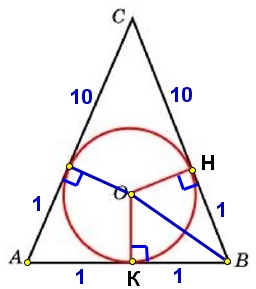
Решение:
По условию СН = 10, НВ = 1. Найдём чему равны боковые стороны равнобедренного ΔАВС:
СВ = АС = СН + НВ = 10 + 1 = 11
Проведём отрезок ОВ:
ΔОНВ = ΔОКВ (ОВ – общая гипотенуза, ∠К = ∠Н = 90º, ОН = ОК, как радиусы), значит соответствующие стороны равны:
НВ = КВ = 1
Найдём основание АВ равнобедренного ΔАВС:
АВ = НВ + КВ = 1 + 1 = 2
Найдём периметр ΔАВС:
РАВС = СВ + СА + АВ = 11 + 11 + 2 = 24
Ответ: 24.