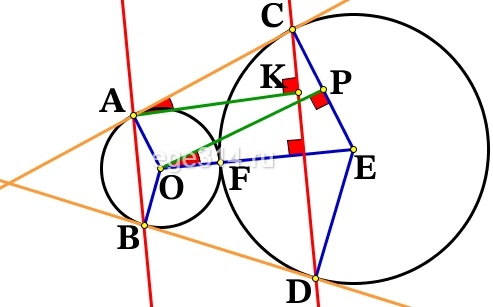
Окружности радиусов 25 и 100 касаются внешним образом. Точки А и В лежат на первой окружности, точки С и D – на второй. При этом АС и ВD – общие касательные окружностей. Найдите расстояние между прямыми АВ и СD.
Источники: Основная волна ОГЭ 2022, ОГЭ Ященко 2022 (50 вар)
Решение:
Построим рисунок по условию, + проведём радиусы: ОA, ОF, OB, EF, EC, ED, построим перпендикуляры AK⊥CD, OP⊥EC:
AK – искомое расстояние между прямыми АВ и CD.
ΔCAK∼ΔPOE, по двум равным углам (∠CKA=∠OPE = 90°, ∠CAK = ∠POE, т.к. АС||OP, AK||OE). Запишем соотношение сторон:
\frac{AC}{OE}=\frac{AK}{OP}
Выразим АК:
AK=\frac{AC\cdot OP}{OE}
Найдём ОЕ, как сумму двух радиусов:
OE = OF + EF = 25 + 100 = 125
AOPC – прямоугольник (EC⊥AC, OA⊥AC, как радиусы и касательная), противоположные стороны равны:
ОА = РС = 25
АС = ОР
Найдём EP, как разность двух радиусов:
EP = EC – PC = EC – OA = 100 – 25 = 75
В прямоугольном ΔОРЕ по теореме Пифагора найдём ОР:
ОР2 = ОE2 – EP2 = 1252 – 752 = (125 – 75)·(125 + 75) = 50·200 = 10000
OP=\sqrt{10000}=100
Найдём искомое расстояние АК:
AK=\frac{AC\cdot OP}{OE}=\frac{100\cdot 100}{125}=\frac{4\cdot 20}{1}=80
Ответ: 80.