Окружности с центрами в точках P и Q пересекаются в точках K и L, причём точки P и Q лежат по одну сторону от прямой KL. Докажите, что PQ⊥KL.
Источник: ОГЭ Ященко 2023 (36 вар)
Решение:
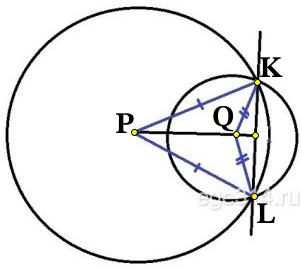
Построим радиусы PK = PL и QK = QL.
Рассмотрим ΔPQK и ΔPQL, в них стороны PK = PL и QK = QL, как радиусы окружностей, сторона PQ общая. ΔPQK = ΔPQL по трём равным сторонам.
Из равенства треугольников ∠KPQ = ∠LPQ, значит прямая PQ является биссектрисой ∠P, в равнобедренном ΔPKL.
Биссектриса равнобедренного треугольника проведённая к основанию так же является и высотой, тогда KL⊥PQ.
Что и требовалось доказать.