Внутри параллелограмма ABCD выбрали произвольную точку K. Докажите, что сумма площадей треугольников АВК и CDK равна половине площади параллелограмма.
Источник: ОГЭ Ященко 2023 (36 вар)
Решение:
Проведём, через произвольную точку K, высоту параллелограмма MH, части которой KM и KH будут являться высотами треугольников:
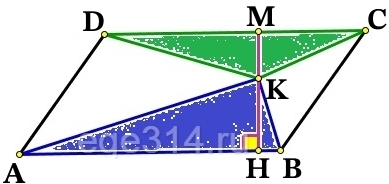
Площадь параллелограмма ABCD находится следующим образом:
S_{ABCD}=AB\cdot MH
Выразим сумму площадей треугольников ΔABK и ΔCDK:
S_{\Delta ABK}+S_{\Delta CDK}=\frac{1}{2}\cdot AB\cdot KH+\frac{1}{2}\cdot DC\cdot KM=\frac{1}{2}\cdot AB\cdot KH+\frac{1}{2}\cdot AB\cdot KM=\frac{1}{2}\cdot AB\cdot (KH+KM)=\frac{1}{2}\cdot AB\cdot MH=\frac{AB\cdot MH}{2}=\frac{S_{ABCD}}{2}
Что и требовалось доказать.