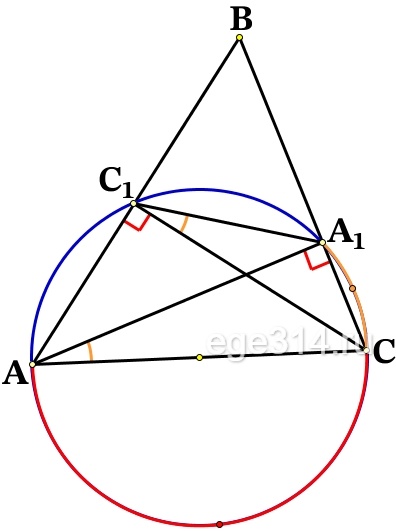
Решение №2293 В остроугольном треугольнике ABC проведены высоты AA1 и CC1.

Решение:

    Если отрезок AС  виден из точек А₁ и C₁, лежащих по одну сторону от прямой AС, под одним и тем же углом (90°), то точки A, С, А₁, С₁ лежат на одной окружности (ΔАС₁С и ΔАА₁С прямоугольные с общей гипотенузой AС, если описать около каждого из них окружность, то АС будет диаметром, а значит окружности совпадут):

    Тогда углы ∠СС₁А₁ и ∠САА₁ вписанные в окружность, опираются на одну и туже дугу ‿A₁С, значит они равны:

∠СС₁А₁ = ∠САА₁

    Что и требовалось доказать.