Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 10, а одна из диагоналей ромба равна 40. Найдите углы ромба.
Источник: ОГЭ Ященко 2023 (36 вар)
Решение:
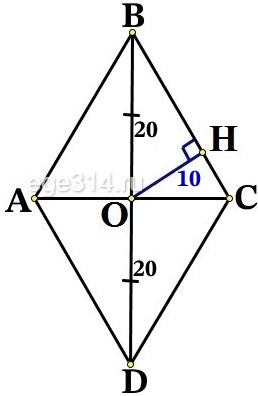
Диагонали ромба в точке пересечения О делятся пополам. Найдём ОВ:
OB=\frac{BD}{2}=\frac{40}{2}=20
Тогда из прямоугольного треугольника ΔBOH, найдём синус ∠OBН как отношение противолежащего катета OН к гипотенузе OB:
sin\angle OBH=\frac{10}{20}=\frac{1}{2}
∠ОВН = 30°
(синус острого угла равен \frac{1}{2}, только если этот угол 30°)
Диагональ BD делит угол В пополам (является биссектрисой по свойству диагоналей ромба), тогда В равен:
∠В = 2·∠ОВН = 2·30° = 60°
Противоположные углы ромба равны:
∠D = ∠В = 60°
Cумма углов ромба равна 360°. Найдём ∠А = ∠С:
\angle A=\angle C=\frac{360°-\angle B-\angle D}{2}=\frac{360°-60°-60°}{2}=\frac{240°}{2}=120°
Ответ: 60°; 60°; 120°; 120°.