Решение №3374 Катеты прямоугольного треугольника равны 10 и 24.

Решение:

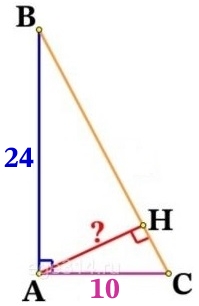
    В прямоугольном ΔАВС, по теореме Пифагора, найдём гипотенузу BC:

АВ² + АС² = ВС²
24² + 10² = ВС²
576 + 100 = ВС²
676 = BC²
BC = √676 = 26

    Найдём площадь ΔАВС (АС – основание, АВ – высота):

S_{\Delta}=\frac{1}{2}\cdot a\cdot h=\frac{1}{2}\cdot AC\cdot AB=\frac{1}{2}\cdot 10\cdot 24=5\cdot 24=120

    Из формулы площади ΔАВС, найдём его высоту АН проведённую к гипотенузе (ВС – основание, АН – высота):

S_{\Delta}=\frac{1}{2}\cdot BC\cdot AH\\120=\frac{1}{2}\cdot 26\cdot AH \\120= 13\cdot AH\\AH=\frac{120}{13}

Ответ: \frac{120}{13}.