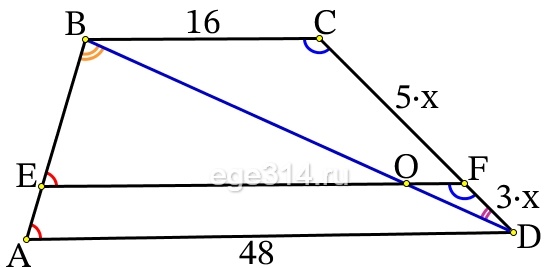
Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD = 48, BC = 16, CF:DF = 5:3.
Источник: ОГЭ Ященко 2022 (36 вар)
Решение:
Проведём диагональ BD трапеции ABCD, которая пересекает прямую EF в точке О:
По условию CF:DF = 5:3, пусть СF = 5x, а DF = 3x, тогда:
СD = CF + DF = 5x + 3x = 8x
Прямая ЕF||AD, ЕF||BC, значит сторону AB она делит в тех же отношениях:
BE = 5y
AE = 3y
AB = 8y
ΔBDC подобен ΔОFD по двум равным углам (∠D – общий, ∠BCD = ∠OFD – как соответственные при двух параллельных прямых и секущей). Из подобия сторон найдём ОF:
\frac{BC}{OF}=\frac{CD}{FD}\\\frac{16}{OF}=\frac{8x}{3x}\\\frac{16}{OF}=\frac{8}{3}\\OF=\frac{16\cdot 3}{8}=6
ΔABD подобен ΔEBO по двум равным углам (∠B – общий, ∠BAD = ∠BEO – как соответственные при двух параллельных прямых и секущей). Из подобия сторон найдём ОE:
\frac{AD}{OE}=\frac{AB}{EB}\\\frac{48}{OE}=\frac{8y}{5y}\\\frac{48}{OE}=\frac{8}{5}\\OE=\frac{48\cdot 5}{8}=30
Найдём EF:
EF = OF + OE = 6 + 30 = 36
Ответ: 36.