Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя 20 минут, когда одному из них оставалось 400 м до окончания первого круга, ему сообщили, что второй бегун прошёл первый круг 1 минуту назад. Найдите скорость первого бегуна, если известно, что она на 2 км/ч меньше скорости второго.
Источник: ОГЭ Ященко 2022 (36 вар)
Решение:
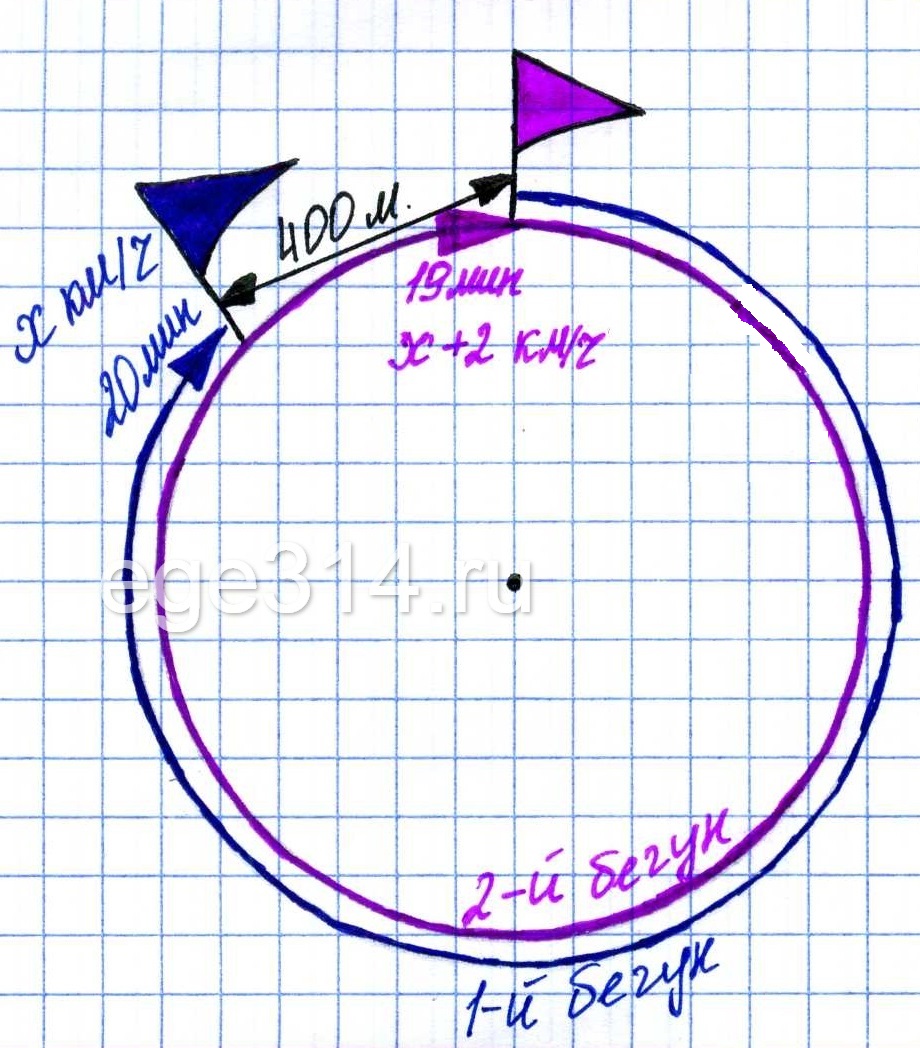
Пусть скорость 1-го бегуна х км/ч, а скорость 2-го бегуна на 2 км/ч больше, т.е. х + 2 км/ч.
Момент в который между ними могло быть известное нам расстояние, это когда 2-й бегун пробежал целый круг за 20 – 1 = 19 минут (\frac{19}{60} ч), а 1-й бегун не добежал 400 метров (0,4 км) до целого круга за 20 минут (\frac{20}{60} ч).
1-й пробежал:
\frac{20}{60}·x
2-й пробежал:
\frac{19}{60}·(x+2)
и это на 0,4 км больше, чем 1-й бегун.
Составим уравнение:
\frac{19}{60}·(x+2)-\frac{20}{60}·x=0,4 |·60
19·(x + 2) – 20x = 24
19x + 38 – 20x = 24
–x = 24 – 38
–x = –14 |·(–1)
x = 14 км/ч
Ответ: 14.