Какое из следующих утверждений верно?
1) Сумма углов выпуклого четырёхугольника равна 360 градусам.
2) Средняя линия трапеции равна сумме её оснований.
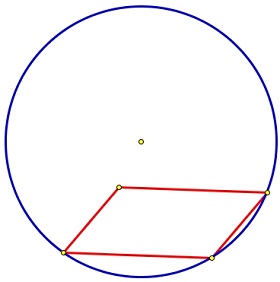
3) Любой параллелограмм можно вписать в окружность.
В ответ запишите номер выбранного утверждении.
Источник: ОГЭ Ященко 2022 (36 вар)
Решение:
1) верно, по теореме о сумме углов выпуклого многоугольника, сумма углов n-угольника равна 180°·(n − 2):
180°·(n − 2) = 180°·(4 − 2) = 180°·2 = 360°
2) не верно, средняя линия трапеции равна полусумме её оснований, а не сумме её оснований;
3) не верно, ниже пример параллелограмма который нельзя вписать в окружность:
Ответ: 1.