Решение №762 Найдите объём правильной четырёхугольной пирамиды, сторона основания …

Решение:

    Из справочного материала знаем площадь пирамиды:

S=\frac{1}{3}\cdot S_{осн}\cdot h

    В основании правильной четырёхугольной пирамиды лежит квадрат:

S_осн = a² = 4² = 16

    Найдём диагональ (d) основания по теореме Пифагора:

d² = a² + a²
d² = 4² + 4²
d² = 16 + 16
d² = 32
d =  \sqrt{32} = 4√2

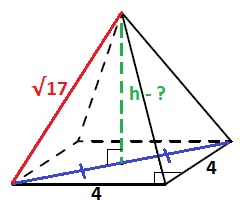
    Рассмотрим прямоугольный треугольник содержащий высоту. В нём гипотенуза равна \color{Red} \sqrt{17}, катет равен половине диагонали, т.е. \frac{4\sqrt{2}}{2}=\color{Blue} 2\sqrt{2}, высоту h найдём по теореме Пифагора:

h² + (2√2)² = (√17)²
h² + 8 = 17
h² = 17 – 8 = 9
h = 3

    Площадь пирамиды:

S=\frac{1}{3}\cdot S_{осн}\cdot h=\frac{1}{3}\cdot 16\cdot 3=16

Ответ: 16.