Радиус окружности, описанной около квадрата, равен 24√2. Найдите радиус окружности, вписанный в этот квадрат.
Источник: ОГЭ Ященко 2023 (36 вар)
Решение:
Проведём радиусы вписанной окружности к квадрату, так, что бы они являлись касательными (радиус перпендикулярен касательной):
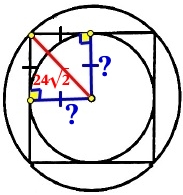
Получаем ещё один квадрат, у него все стороны равны радиусу вписанной окружности, все углы прямые. Диагональ этого квадрата, является радиусом описанной окружности около исходного квадрата и равна 24√2.
В прямоугольном треугольнике, по теореме Пифагора, найдём искомый радиус:
(24√2)2 = r2 + r2
576·2 = 2r2 |:2
576 = r2
r = √576 = 24
Ответ: 24.