Точки М и N являются серединами сторон АВ и ВС треугольника АBС соответственно. Отрезки АN и СМ пересекаются в точке О, АN = 24, СМ = 9. Найдите СО.
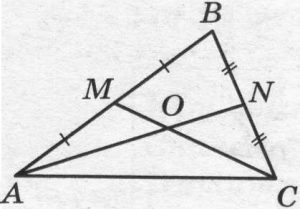
Источник: ОГЭ Ященко 2023 (50 вар)
Решение:
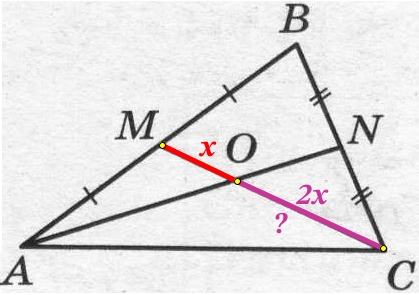
Т.к. точки М и N являются серединами сторон АВ и ВС, то AN и CM это медианы.
По свойству медианы: Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины.
Тогда отрезки отрезки медианы СМ относятся как СО:ОМ = 2:1. Обозначим ОМ как х, тогда СО 2х:
ОM + СО = СМ
х + 2х = 9
3х = 9
х = 9/3 = 3
Найдём СО:
СО = 2х = 2·3 = 6
Ответ: 6.