Ваня летом отдыхает у дедушки и бабушки в деревне Николаевке. Ваня с дедушкой собираются съездить на велосипедах в село Игнатьево на железнодорожную станцию. Из Николаевки в Игнатьево можно проехать по шоссе до деревни Сосновки, где нужно свернуть под прямым углом направо на другое шоссе, ведущее в Игнатьево через посёлок Дачный. Из Николаевки в Игнатьево можно проехать через посёлок Дачный и не заезжая в Сосновку, но тогда первую часть пути надо будет ехать по прямой лесной дорожке. Есть и третий маршрут: доехать по прямой тропинке мимо озера до деревни Кулички и там, повернув налево, по шоссе добраться до Игнатьево.
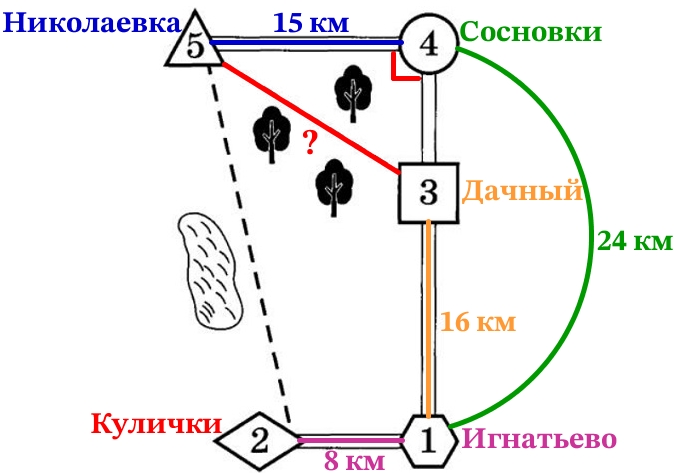
По шоссе Ваня с дедушкой едут со скоростью 20 км/ч, а по лесной дорожке и тропинке – 15 км/ч. Расстояние по шоссе от Николаевки до Сосновки равно 15 км, от Игнатьево до Сосновки – 24 км, от Игнатьево до Дачного – 16 км, а от Игнатьево до Куличек – 8 км.
Источник: ОГЭ Ященко 2023 (36 вар)
Задание 1
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответ запишите полученную последовательность пяти цифр.
Решение:
Из Николаевки (5) в Игнатьево можно проехать по шоссе до деревни Сосновки (4), где нужно свернуть под прямым углом направо на другое шоссе, ведущее в Игнатьево (1) через посёлок Дачный (3). Из Николаевки (5) в Игнатьево (1) можно проехать через посёлок Дачный (3) и не заезжая в Сосновку (4), но тогда первую часть пути надо будет ехать по прямой лесной дорожке. Есть и третий маршрут: доехать по прямой тропинке мимо озера до деревни Кулички (2) и там, повернув налево, по шоссе добраться до Игнатьево (1).
Ответ: 51432.
Задание 2
На сколько процентов скорость, с которой едут Ваня с дедушкой по тропинке, меньше их скорости по шоссе?
Решение:
По шоссе скорость: 20 км/ч
По тропинке скорость: 15 км/ч
Скорость по тропинке меньше скорости по шоссе на:
20 – 15 = 5 км/ч
20 км/ч это 100%, найдём сколько от этого составляют 5 км/ч:
\frac{5}{20}\cdot 100\%=\frac{1}{4}\cdot 100\%=0,25\cdot 100\%=25\%
Ответ: 25.
Задание 3
Найдите расстояние от деревни Николаевки до посёлка Дачного по лесной дорожке. Ответ дайте в километрах.
Решение:
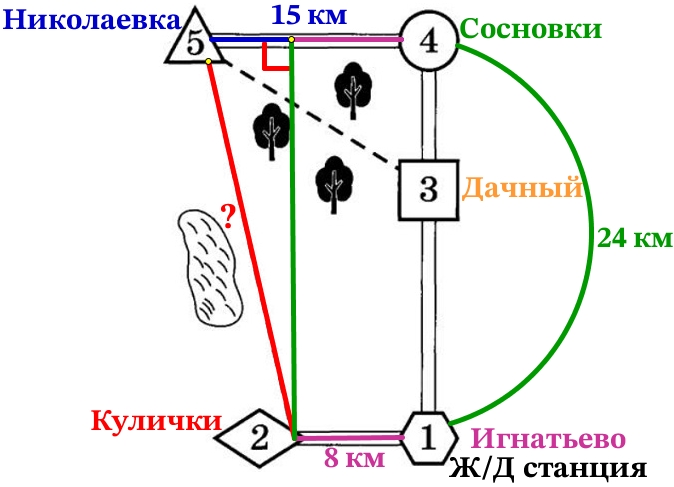
Рассмотрим прямоугольный треугольник.
В нём меньший катет равен разнице между расстояниями Сосновки – Игнатьево и Сосновки – Дачный:
24 – 16 = 8 км
Больший катет равен расстоянию между Николаевка – Сосновки т.е. 15 км.
Гипотенуза это искомое расстояние Николаевка – Дачный (х), найдём по теореме Пифагора:
х2 = 82 + 152
х2 = 64 + 225
х2 = 289
х = √289 = 17 км
Ответ: 17.
Задание 4
Сколько минут затратят на дорогу Ваня с дедушкой, если поедут на станцию через Сосновку?
Решение:
Маршрут проходит по шоссе и состоит из Николаевка – Сосновка 15 км и Сосновка – Игнатьево 24 км:
15 + 24 = 39 км
Скорость по шоссе равна 20 км/ч, тогда затраченное время равно:
\frac{39}{20} часа
Найдём сколько это в минутах (1 час = 60 минут):
\frac{39}{20}\cdot 60=39\cdot 3=117
Ответ: 117.
Задание 5
Определите, на какой маршрут до станции потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Ваня с дедушкой, если поедут этим маршрутом.
Решение:
1-й маршрут по шоссе по шоссе состоит из Николаевка – Сосновка и Сосновка – Игнатьево, на него потратят t1 = 117 минут (см. задание 4).
2-й маршрут Николаевка – Дачный по тропинке 17 км со скоростью 15 км/ч и Дачный – Игнатьево по шоссе 16 км со скоростью 20 км/ч:
t_{2}=\frac{17}{15}+\frac{16}{20}=\frac{17}{15}+\frac{4}{5}=\frac{17\cdot 1+4\cdot 3}{15}=\frac{17+12}{15}=\frac{29}{15} часа
Найдём сколько это в минутах:
\frac{29}{15}\cdot 60=29\cdot 4=116 минут
Найдём расстояние Николаевка – Куличи из прямоугольного треугольника.
В нём меньший катет равен разнице между расстояниями Николаевка – Сосновки и Куличи – Игнатьево:
15 – 8 = 7 км
Больший катет равен расстоянию между Сосновки – Игнатьево т.е. 24 км.
Гипотенуза это искомое расстояние Николаевка – Куличи (х), найдём по теореме Пифагора:
х2 = 72 + 242
х2 = 49 + 576
х2 = 625
х = √625 = 25 км
3-й маршрут Николаевка – Куличи по тропинке 25 км со скоростью 15 км/ч и Куличи – Игнатьево по шоссе 8 км со скоростью 20 км/ч:
t_{2}=\frac{25}{15}+\frac{8}{20}=\frac{5}{3}+\frac{2}{5}=\frac{5\cdot 5+2\cdot 3}{15}=\frac{25+6}{15}=\frac{31}{15} часа
Найдём сколько это в минутах:
\frac{31}{15}\cdot 60=31\cdot 4=124 минут
Меньше всего времени Ваня с дедушкой потратят на 2-й маршрут – 116 минут.
Ответ: 116.