Две подруги Оля и Таня задумались о том, как рассчитать площадь поверхности зонта.
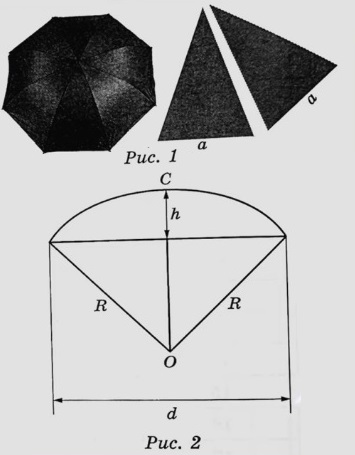
На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из двенадцати отдельных клиньев, натянутых на каркас из двенадцати спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.
Оля и Таня сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 28 см. Высота купола зонта h (рис. 2) оказалась равна 27 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, – ровно 108 см.
Источник: ОГЭ Ященко 2023 (36 вар)
Задание 1
Длина зонта в сложенном виде равна 27 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,8 см.
Решение
Найдём треть длины спицы, отняв от длины всего зонта длину ручки:
27 см – 6,8 см = 20,2 см
Если это треть, то вся спица в 3 раза больше:
20,2·3 = 60,6 см
Ответ: 60,6.
Задание 2
«Поскольку зонт сшит из треугольников, – рассуждала Оля, – площадь его поверхности можно найти как сумму площадей треугольников». Вычислите площадь поверхности зонта методом Оли, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 59 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.
Решение
По первому условию зонт состоит из 12 треугольников с основанием а = 28 см и высотой h = 59 см.
Площадь одного такого треугольника:
S_{\Delta}=\frac{1}{2}ah=\frac{1}{2}\cdot 28\cdot 59=14\cdot 59=826
Найдём площадь поверхности зонта, методом Оли, округлив до ДЕСЯТКОВ:
Sповерхности = 12·SΔ = 12·826 = 9912 ≈ 9910 см2
Ответ: 9910.
Задание 3
Таня предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что ОС = R (рис. 2). Ответ дайте в сантиметрах.
Решение
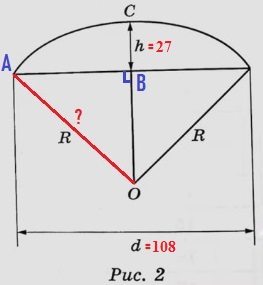
Нам необходимо найти гипотенузу R в прямоугольном треугольнике АВО. АВ равно половине d:
AB = d/2 = 108/2 = 54
Т.к. по условию ОС = R, то:
ОВ = ОС – h = R – 27
По теореме Пифагора найдём ОА = R:
ОА2 = АВ2 + ОВ2
R2 = 542 + (R – 27)2
R2 = 2916 + R2 – 54R + 729
R2 – R2 + 54R = 3645
54R = 3645
R = 3645/54 = 67,5
Ответ: 67,5.
Задание 4
Таня нашла площадь купола зонта как площадь поверхности сферического сегмента по формуле S = 2πRh‚ где R – радиус сферы, а h – высота сегмента. Рассчитайте площадь поверхности купола способом Тани. Число π округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.
Решение
S = 2πRh
π ≈ 3,14
R = 67,5
h = 27
Найдём площадь и округлим до целого:
S = 2πRh = 2·3,14·67,5·27 = 54·3,14·67,5 = 11445,3 ≈ 11445 см2
Ответ: 11445.
Задание 5
Рулон ткани имеет длину 20 м и ширину 90 см. На фабрике из этого рулона были вырезаны треугольные клинья для 15 зонтов, таких же, как зонт, который был у Оли и Тани. Каждый треугольник с учётом припуска на швы имеет площадь 850 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?
Решение:
Найдём площадь рулона ткани в см2:
S = 20м х 90см = 2000см х 90см = 180000 см2
Помня, что в одном зонте 12 треугольников найдём сколько ушло ткани на 15 зонтов:
S1 = 15·12·850 = 153000 см2
Найдём сколько см2 ткани рулона ушло в обрезки:
S2 = S – S1 = 180000 – 153000 = 27000 см2
Найдём сколько это процентов от начального рулона:
\frac{27000}{180000}\cdot 100\%=\frac{27}{180}\cdot 100\%=\frac{3}{20}\cdot 100\%=\frac{3 \cdot 100}{20}\%=\frac{3 \cdot 5}{1}\%=15\%
Ответ: 15.